SLEPLET: Slepian Scale-Discretised Wavelets in Python

SLEPLET is a Python package for the construction of Slepian wavelets in the spherical and manifold (via meshes) settings. In contrast to other codes, SLEPLET handles any spherical region as well as the general manifold setting. The API is documented and easily extendible, designed in an object-orientated manner. Upon installation, SLEPLET comes with two command line interfaces - sphere and mesh - that allow one to easily generate plots on the sphere and a set of meshes using plotly. Whilst these scripts are the primary intended use, SLEPLET may be used directly to generate the Slepian coefficients in the spherical/manifold setting and use methods to convert these into real space for visualisation or other intended purposes. The construction of the sifting convolution was required to create Slepian wavelets. As a result, there are also many examples of functions on the sphere in harmonic space (rather than Slepian) that were used to demonstrate its effectiveness. SLEPLET has been used in the development of several papers.

Background

Wavelets are widely used in various disciplines to analyse signals both in space and scale. Whilst many fields measure data on manifolds (i.e. the sphere), often data are only observed on a partial region of the manifold. Wavelets are a typical approach to data of this form, but the wavelet coefficients that overlap with the boundary become contaminated and must be removed for accurate analysis. Another approach is to estimate the region of missing data and to use existing whole-manifold methods for analysis. However, both approaches introduce uncertainty into any analysis. Slepian wavelets enable one to work directly with only the data present, thus avoiding the problems discussed above. Applications of Slepian wavelets to areas of research measuring data on the partial sphere include gravitational/magnetic fields in geodesy, ground-based measurements in astronomy, measurements of whole-planet properties in planetary science, geomagnetism of the Earth, and cosmic microwave background analyses.

Statement of Need

Many fields in science and engineering measure data that inherently live on non-Euclidean geometries, such as the sphere. Techniques developed in the Euclidean setting must be extended to other geometries. Due to recent interest in geometric deep learning, analogues of Euclidean techniques must also handle general manifolds or graphs. Often, data are only observed over partial regions of manifolds, and thus standard whole-manifold techniques may not yield accurate predictions. Slepian wavelets are designed for datasets like these. Slepian wavelets are built upon the eigenfunctions of the Slepian concentration problem of the manifold: a set of bandlimited functions that are maximally concentrated within a given region. Wavelets are constructed through a tiling of the Slepian harmonic line by leveraging the existing scale-discretised framework. Whilst these wavelets were inspired by spherical datasets, like in cosmology, the wavelet construction may be utilised for manifold or graph data.

To the author’s knowledge, there is no public software that allows one to compute Slepian wavelets (or a similar approach) on the sphere or general manifolds/meshes. SHTools is a Python code used for spherical harmonic transforms, which allows one to compute the Slepian functions of the spherical polar cap. A series of MATLAB scripts exist in slepian_alpha, which permits the calculation of the Slepian functions on the sphere. However, these scripts are very specialised and hard to generalise.

Whilst Slepian wavelets may be trivially computed from a set of Slepian functions, the computation of the spherical Slepian functions themselves are computationally complex, where the matrix scales as 𝒪(𝐿⁴). Although symmetries of this matrix and the spherical harmonics have been exploited, filling in this matrix is inherently slow due to the many integrals performed. The matrix is filled in parallel in Python using concurrent.futures, and the spherical harmonic transforms are computed in C using SSHT. This may be sped up further by utilising the new ducc0 backend for SSHT, which may allow for a multithreaded solution. Ultimately, the eigenproblem must be solved to compute the Slepian functions, requiring sophisticated algorithms to balance speed and accuracy. Therefore, to work with high-resolution data such as these, one requires high-performance computing methods on supercomputers with massive memory and storage. To this end, Slepian wavelets may be exploited at present at low resolutions, but further work is required for them to be fully scalable.

Example Usage

SLEPLET may be interacted with via the API or the CLIs.

API Usage

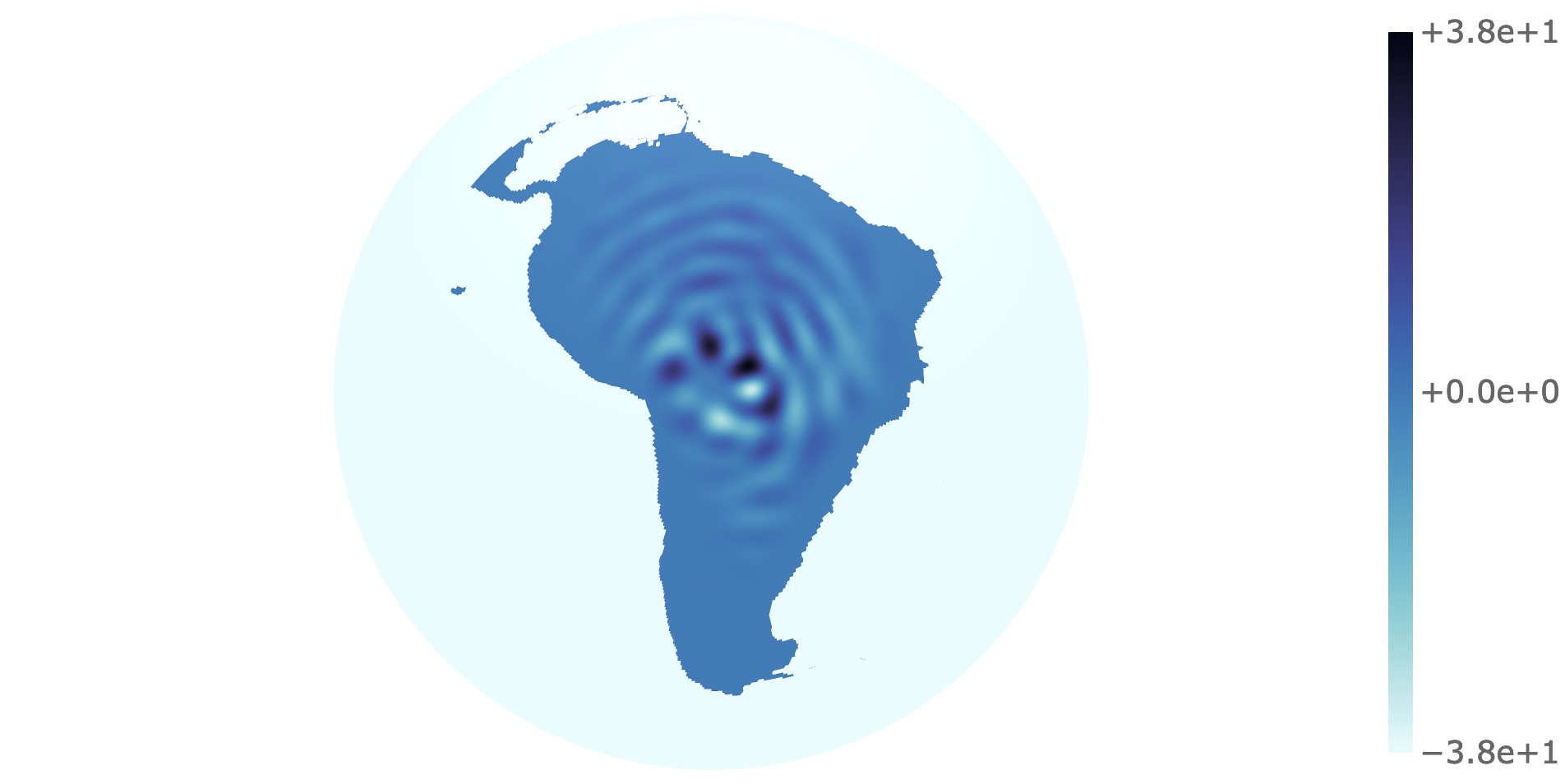
The following demonstrates the first wavelet (ignoring the scaling function) of the South America region on the sphere.

import sleplet

B, J, J_MIN, L = 3, 0, 2, 128

region = sleplet.slepian.Region(mask_name="south_america")
f = sleplet.functions.SlepianWavelets(L, region=region, B=B, j_min=J_MIN, j=J)
f_sphere = sleplet.slepian_methods.slepian_inverse(f.coefficients, f.L, f.slepian)
sleplet.plotting.PlotSphere(
    f_sphere,
    f.L,
    f"slepian_wavelets_south_america_{B}B_{J_MIN}jmin_{J_MIN+J}j_L{L}",
    normalise=False,
    region=f.region,
).execute()

CLI Usage

The demonstrates the first wavelet (ignoring the scaling function) of the head region of a Homer Simpson mesh for a per-vertex normals field.

mesh homer -e 3 2 0 -m slepian_wavelet_coefficients -u -z

Citing

If you use SLEPLET in your research, please cite the paper.

@article{Roddy2023,
  title   = {{SLEPLET: Slepian Scale-Discretised Wavelets in Python}},
  author  = {Roddy, Patrick J.},
  year    = 2023,
  journal = {Journal of Open Source Software},
  volume  = 8,
  number  = 84,
  pages   = 5221,
  doi     = {10.21105/joss.05221},
}

Please also cite S2LET upon which SLEPLET is built, along with SSHT in the spherical setting or libigl in the mesh setting.

Acknowledgements

The author would like to thank Jason D. McEwen for his advice and guidance on the mathematics behind SLEPLET. Further, the author would like to thank Zubair Khalid for providing his MATLAB implementation to compute the Slepian functions of a polar cap region, as well as the formulation for a limited colatitude-longitude region. SLEPLET makes use of several libraries the author would like to acknowledge, in particular, libigl, NumPy, plotly, SSHT, S2LET.